2019 학년도 9월 모평 6번#

거리는 다른데 A, B가 동시에 도착한다

• ㄱ X - $v_b > v_a$ 이고 $t$는 일정하므로 $\bar{v}$은 $B$가 더 크다.
• ㄴ X - 가속도 $a$는 $\frac{\Delta v}{t}$ 이므로 $B$가 $A$보다 크다.
• ㄷ O - 역학적 에너지 감소량은 아래와 같이 계산할 수 있다.
  $-mgh$는 $A$, $B$가 모두 같다.
  $E_k$를 계산하면
  • $E_ka = \frac{1}{2}m(v_a)^2$
  • $E_kb = \frac{1}{2}m(v_b)^2$
  • $v_b > v_a$ 이므로 $E_kb > E_ka$ 따라서 A가 역학적 에너지를 더 많이 잃었다

답: 2

2019 학년도 9월 모평 14번#

가속도가 $10m/s^2$ 으로 같다 $A, B$의 $a$, $s$, $v_i$가 주어지므로 $t$와 $v_f$를 구해낼 수 있다.

ㄱ O

A의 초기 속력은 $20m/s$, B의 초기 속력은 $10m/s$이다.
이 둘은 중력가속도 $10m/s^2$을 받아 $2$초 후에 충돌한다.
즉 A의 나중 속력은 $40m/s$, B의 나중 속력은 $30m/s$이다.

ㄴ O

운동량은 $P=mv$로 구할 수 있다

• $P_{A,i} = 20 \cdot 1 = 20$, $P_{A,f} = 40 \cdot 1 = 40$
• $P_{B,i} = 10 \cdot 1 = 10$, $P_{B,f} = 30 \cdot 1 = 30$
• $\Delta P$는 $20kg \cdot m/s$로 같다.

ㄷ O

$v_{A,i} = 20m/s$, $v_{A, f} = 40m/s$ 이므로 $\bar{v_A}$는 $30m/s$가 된다.
$\bar{v_A} \cdot t = 30 \cdot 2 = 60 = s$
$m \cdot g \cdot s = 1 \cdot 10 \cdot 60 = 600$
충돌할 때 까지 2초가 걸렸으므로 A가 2초 동안 이동한 거리에 mg를 곱하면 $E_k$의 감소량을 구할 수 있다.

답: 5

오투 대수능 대비 특별자료 실전 예상 모의고사 3회 5번#

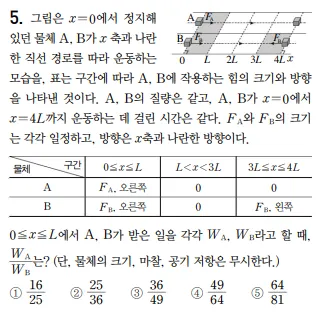
인텐은 역학적 에너지로 푸는거 같은데 그냥 v-t 그려서 풀었다

A의 속력을 $v_A$, 시간을 $t_1$
B의 속력을 $v_B$, 시간을 $t_2$ 라고 정의할 때 거리가지고 계산해보면 각각 도달한 시간을 구할 수 있다. $A$는 $\frac{5}{2} t_1$, $B$는 $3t_2$ 걸려서 도착한다.

• 문제에서 $4L$까지 운동하는데 걸린 시간이 같다고 명시되어 있으므로
  $\frac{5}{2} t_1 = 3t_2$

• 같은거리 $L$을 이동할 때를 가지고 식을 세우면
  $v_A \cdot t_1 = v_B \cdot t_2$

• 두 물체의 질량이 같고 이동한 거리가 같으므로
  $\frac{W_A}{W_B} = \frac{F_A}{F_B} = \frac{a_A}{a_B}$

세 식을 모두 정리하면 $\frac{25}{36}$이 나온다

답: 2

2022 학년도 9월 모평 20번#

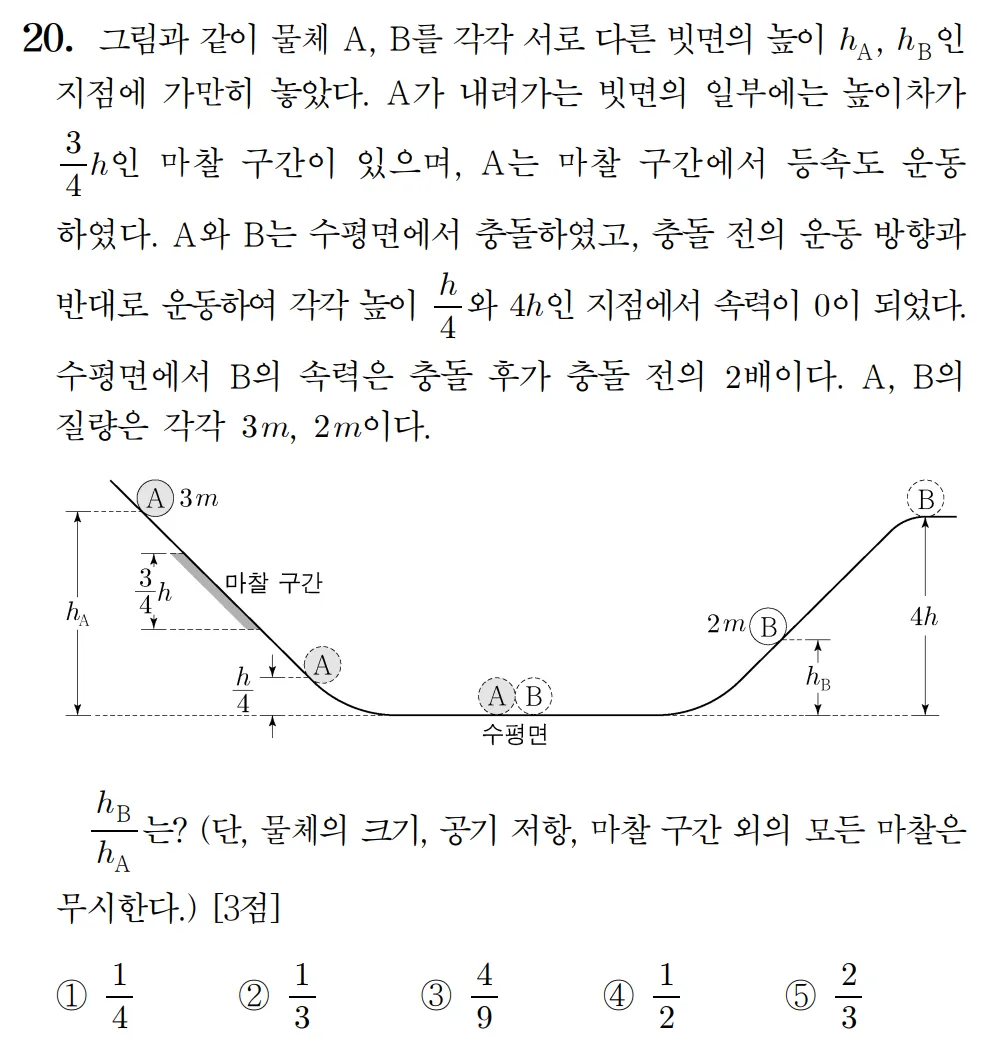
간단하게 마찰구간 빼고 역학적 에너지 보존으로 풀어주면 된다.

$E_{A,i} + E_{B,i} - E_{\text{손실}} = E_{A,f} + E_{B,f}$
$3m \cdot g \cdot h_A + 2m \cdot g \cdot h_B - \frac{3}{4}h\cdot 3m \cdot g = \frac{h}{4} \cdot 3m \cdot g + 4h \cdot 2m \cdot g$

정리하면 아래와 같은 식을 구해낼 수 있다

• $3h_A + 2h_B = 11h$

문제에서 B의 속력은 충돌 후가 충돌 전의 2배라고 한다 이를 이용해 식을 더 도출해낼 수 있다

• $4h \cdot 2m \cdot g = \frac{1}{2} \cdot 2m \cdot (2v_B)^2$
• $2m \cdot g \cdot h_B = \frac{1}{2} \cdot 2m \cdot (v_B) ^2$

정리하면

• $v_B^2 = 2gh$
• $v_B^2 = 2gh_B$

$h=h_B$

따라서 $h_A = 3h_B$가 되어 답은 $\frac{1}{3}$이다.

답: 2

2021 학년도 10월 학평 20번#

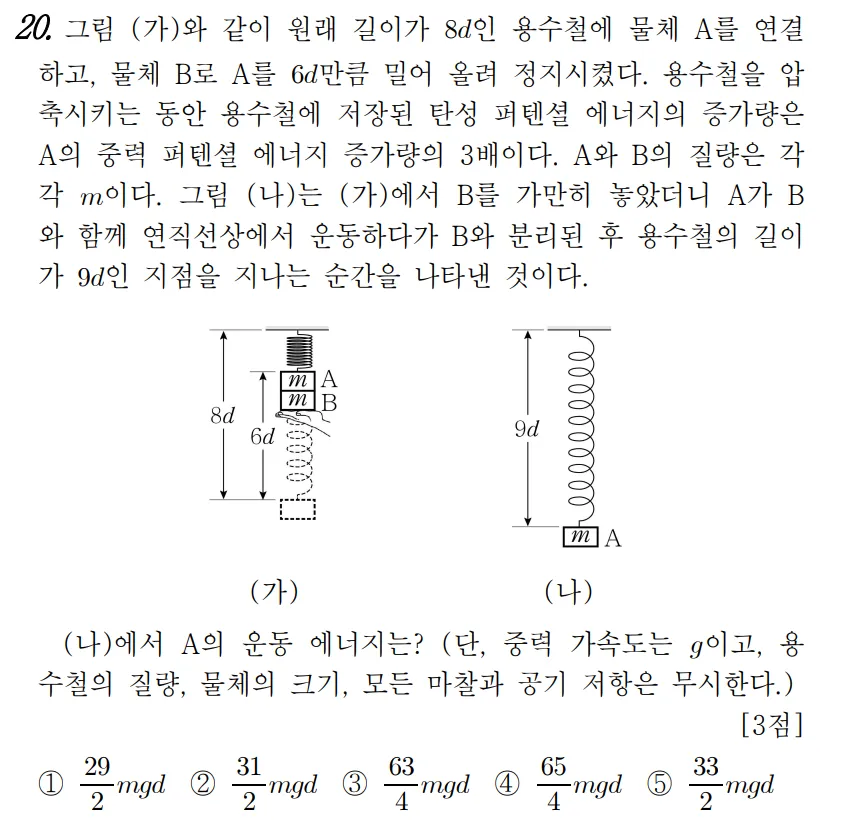
그림이랑 물체 동작 이해하는게 좀 어려웠다.

기준면을 (가)의 물체 윗부분으로 보고 시작한다

$E_pA = 6mgd, E_pB = 6mgd$ 이다.
$E_{\text{탄성}} = 3E_pA = 18mgd (=\frac{1}{2} \cdot k \cdot (6d)^2)$

역학적 에너지 $E$는 $30mgd$이고 $A$와 $B$의 질량이 같으므로 각각 $15mgd$씩 나눠 가진다
$E_A = 15mgd, E_B = 15mgd$

또, $\frac{1}{2}k \cdot (6d)^2 = 18mgd$
$kd=mg$임을 도출해낸다.
$E_A = A의 E_{\text{탄성p}} + E_{\text{중력p}} + E_k$이다.

(나) 그림을 봤을 때 A는 기준면 보다 d만큼 더 내려가 있으므로 $E_{\text{중력p}} = -mgd$

$15mgd = \frac{1}{2}mgd - mgd + E_k$

따라서 $E_k = \frac{31}{2}mgd$

답: 2

2024 학년도 수능 20번#

세 과정이 필요하다

??? 학년도 ?? 20번#

문제는 나중에 첨부하겠다

A 초기 속력: 4v, 나중 속력: v,
B 초기 속력: $v_B$, 나중 속력: $v_B'$ 이라고 정의한다.